はじめに
ここでは、アルゴリズムの主に探索と並び替えをテーマにしていきます。
アルゴリズムとは、問題解決のための手順です。
例えば料理を作るという問題においては、その料理を作るための材料が与えられて、レシピの手順通りに調理をし、最終的に料理が完成します。レシピも一種のアルゴリズムと言えるでしょう。
また、紙の電話帳からお店の連絡先(仮にtechportとする)を探し出すのもアルゴリズムです。
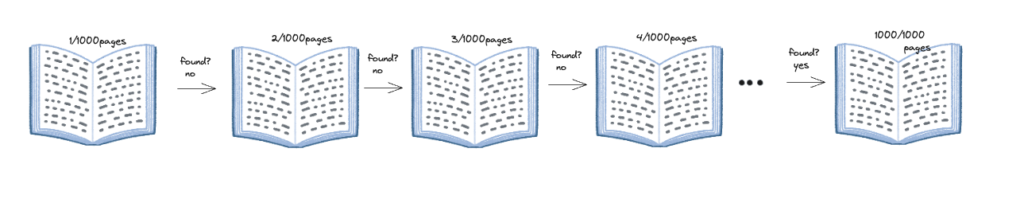
電話帳が全部で1000ページあるとき、一ページ目から確認していけばいつかは”techport”を探し出すこともできるでしょう。ですがこれは果たしてよい方法でしょうか?
めくるページが一ページずつではなく、二ページずつにした場合はどうでしょう?
この場合、もしかしたら当たりのページを読み飛ばしてしまいます。ですが、電話帳は通常、一定の順番通りに並んでいるものです。もし今開いているページが”tf…”のように順番的に飛ばしてしまっていると判断できるとき、一つ前のページに戻るなんてことを行えば、読み飛ばして最後までページを開いても探し出すことができなかったという事態は防ぐことができます。
一ページずつ飛ばしてページをめくるのではなく、二ページずつめくることで、およそ検索にかかる時間は二分の一になるでしょう。これを三ページ、四ページとめくる枚数を増やすことでさらに検索にかかる時間は減っていくことでしょう。
ですが、もっとよい方法があります。
アルゴリズムを考えるときは、まず正確に欲しい結果が得られることは大前提としつつも、その効率の良さ(実行時間)というのも重要な要素です。
実行時間
電話帳の一ページ目から特定の情報を一ページずつめくるように、配列の0番目から最後までを順番に見ていく方法を線形探索と言います。
線形探索の実行時間について考えていきましょう。
まず、実行時間とはアルゴリズムを実行するのにかかる時間のことです。
電話帳の例でいうと、1000ページを一枚ずつめくって確かめる方法で、一ページを確かめるのに1秒かかる場合、もっとも遅くて実行時間は1000秒かかります。また、2ページずつめくって確かめる場合は、500秒かかります。
実行時間は与えられた問題の大きさによって同じアルゴリズムを用いても時間が変わってしまうので、問題の大きさはnとして表現されます。
線形探索の実行時間にnを用いた場合、
1ページずつめくる線形探索はn
2ページずつめくる線形探索はn/2
となります。
実行時間を記述するより学術的な表現にビッグO表記があります。
この表記で線形探索を表現するとO(n)となります。
これは2ページずつめくる線形探索であっても同じO(n)です。
ビッグO表記は実行時間の最も支配的な要因にのみ着目しようというものだからです。
つまり、仮にnを2で割っているのだとしてもnの大きさが2倍、3倍に増えれば、それに伴って実行時間も2倍、3倍に増えるのだから、もう2で割るというのは無視してしまっていいでしょということです。
ビッグO表記は最も実行時間がかかる場合の大きさに着目しますが、
反対に実行時間が最も短くなる場合に着目した学術的な表現もあります。ビッグΩ表記です。
線形探索においてはΩ(1)となります。
電話帳の一ページ目に目当ての情報を見つけることができたとき、その時点で検索を終了できるので、最短の実行時間は問題の大きさに関わらず1にできるためです。
バイナリ検索(二分探索)
電話帳の検索の例でいくと、線形探索よりももっと効率的な検索が可能です。
電話帳はアルファベット順などの一定のルールに沿ってページが構成されているため、今自分が開いているページが目的の情報に対して通り過ぎているのか、まだなのかを知ることができます。つまり、目的の情報が現在のページより右側にあるのか、左側にあるのかがわかります。
これを利用して、
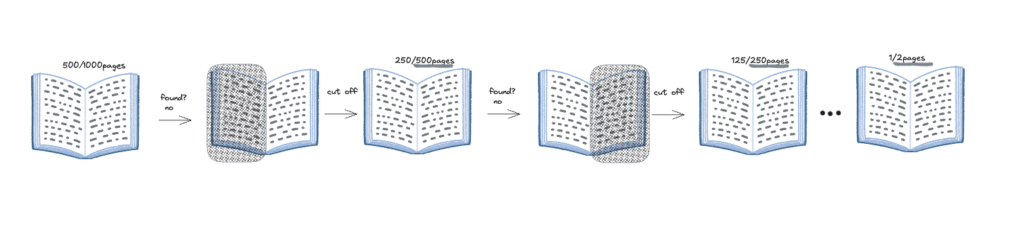
まず電話帳のちょうど真ん中を開いてみます。
そして、そこに目的の情報があるか。ない場合は目的の情報は電話帳の右側なのか左側なのかを判断します。
右側にあるとわかれば、左側は不要なので、切り取って捨てます。
そして、右側のちょうど真ん中を開きます。
そこに情報があるか。ない場合は目的の情報は右側なのか左側なのかを判断します。
左側にあるとわかれば右側は不要なので、切り取って捨てます。
….
これを繰り返すと最終的にページは1枚になり、そしてそのページに情報は存在するはずです。
この検索方法をバイナリ検索(二分探索)といいます。
電話帳のページ数が1024ページある場合、ちょうど10回ページをめくると一枚に特定できるようになります。計算の方法はlog₂1024 = 10です。
nに直すと、log₂n です。
ビッグO表記では、O(log n)と表現されます。(底は省略されます)
対数的に増えていくことの威力は、仮に電話帳のページ数が2倍、3倍と増えていったとしても、検索の回数は1回、2回としか増えないことです。
線形探索に比べると非常に効率がいいですね。
ビッグΩ表記においても、一度目のちょうど真ん中のページに目当ての情報が記載されていればそこで検索を終了できるので、Ω(1)となります。
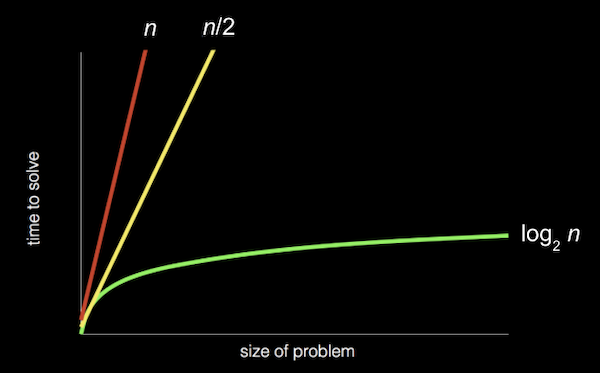
線形探索とバイナリ検索の実行時間の推移をグラフにするとこのようになります。
横軸がデータ量 縦軸が実行時間を表しています。
ソート
電話帳の検索アルゴリズムにおいて、バイナリ検索が優秀でしたが、もし、情報がランダムに配置されている場合はどうでしょう?
その場合には真ん中を開いてみても、右側に情報があるのか左側に情報があるのか、現在開いているページから判断することができなくなります。
そのため、線形探索をすることになってしまいます。
そこで、バイナリ検索ができるように事前にデータを並べ替え(ソート)てしまえばよいです。
次はランダムな配列からソートされた配列を作成するアルゴリズムについて考えていきましょう。
#include <stdio.h>
int main(void)
{
int numbers[] = {6, 3, 8, 5, 2, 7, 4, 1};
// do something
printf(numbers);
// [1, 2, 3, 4, 5, 6, 7, 8]
}
選択ソート
まず、ソートのアルゴリズムを考えるにあたり、コンピュータ上の制約を理解しておきましょう。
私たちはソースコードに数字の配列の定義をみたら、全ての値をパッとみることができ、全体の雰囲気や一番小さい数字、大きい数字をみてとることができますが、コンピュータの目線はそうではありません。
RAMで紹介したようにメモリの中に値があり、その中身をざっと全て確認することはできず、一つ一つ取り出してあげることでそこにどんな値があるのかを知ることができます。要は箱の中に数字が入っていて、箱を開けてあげないと中の数字が確認できないようなイメージです。

そのような制約の中でどのように並べ替えを行うかを検討する必要があります。
もっとも単純な方法は
一番左から数字を一つ一つみていって、その過程で一番小さい値を記憶しておく
数字が最後までいったら、記憶しておいた一番小さい値と一番左端の値を入れ替える。
これにより一番左端に一番小さい値が入ったので、今度は左から2番目から順に一つ一つ数字をみていき、その中で一番小さい値を記憶しておく。
最後まで見終わったら左から2番目の値と一番小さい値を入れ替える。
これにより、左端の2つが小さい順になります。
また、今度は左から3番目から順に一つ一つ数字をみて、その中で一番小さい値を記憶して、左から3番目の値と入れ替える …を繰り返し、
起点が最後の値になるまで繰り返すとソートが完了します。

このサイトで選択ソートで並び替えられる過程をアニメーションで見ることができます。
これから紹介するバブルソートとマージソートについてもアニメーションで確認することができます。イメージをつけるのに利用してみてください
選択ソートの実行時間は1〜8の数字の場合、最初は8回、次に7回、6回…と並び替えが行われていきます。nに置き換えるとn + (n – 1) + (n – 2)…. + 1となります。
このような数列の式はn(n + 1)/2と表現されます。
これを展開するとn^2/2 + n/2となります。
ビッグO表記に直す際にはn/2やn^2を2で割る値は無視して、
O(n^2)と表現されます。
ビッグΩ表記では、完全にソートされた配列だったとしてもそれが完全にソートされている配列だと判断するために同じことを最後まで行う必要があるので、ビッグOと同じく
Ω(n^2)となります。
やっていることはシンプルですが、nの2乗はデータ量が少しでも増えてしまうとあっという間にとてつもない実行時間が必要になってしまいます。
もっとよい方法を検討したいですね。
バブルソート
バブルソートと呼ばれる別のアルゴリズムを検討してみましょう。
バブルソートはまず、一番左端の数字とそれの一つ隣の数字をみて、その二つの数字が順番通りに並んでいるならそのまま。並んでいないなら入れ替えます。
次にまた一番左端とその隣の数字を見て、その二つの数字が順番通りならそのまま、並んでいないなら入れ替える
次にまた一番左端とその隣の数字を見て….を繰り返し、最後から2番目の数字が起点になるまで繰り返します。
(最後の数字が起点になってしまうとその一つ隣の数字はない。RAM上の全く関係ない値を取り出してしまうので、行ってはいけない)
繰り返しの中で一度も入れ替え作業が発生しなくなったらソート完了です。
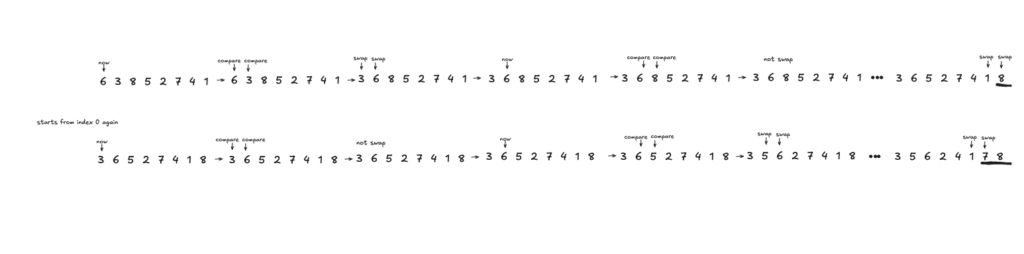
配列の中の一番大きな値がどんどん右に泡のように押し出されるように移動していくことからバブルソートと呼ばれているようです。
8個の配列をバブルソートする場合、一番最初は最大7回入れ替えを行います。また、最大7週することでソートが完了します。nにすると(n – 1)(n – 1) = n^2 – 2n + 2です。
ビッグO表記にすると、2nや2はn^2の前では無視してよい値とみて、
O(n^2)となります。
ビッグOでは選択ソートと変わりはないという結果になってしまいました。
ですが、ビッグΩにおいては、最初からソートされている場合、一度も入れ替え作業を行うことなく、最初の入れ替えチェックが行われるため、そこで終了できます。nにするとn – 1となります。
-1は無視してΩ(n)となります。
ビッグΩは大きな改善ができました。
ですが、やはり最大実行時間がn^2というのは辛いです。
これを改善する方法を検討してみましょう。
マージソート
マージソートと呼ばれるアルゴリズムを検討します。
マージソートは配列の左半分と右半分に分けてさらに分け、さらに分けたうちの右半分と左半分にわけ…を繰り返して、一つの数字になるまで繰り返します。左半分の一つの数字と右半分の一つの数字を見比べて、その数字を小さい順に並べます。これを繰り返します。
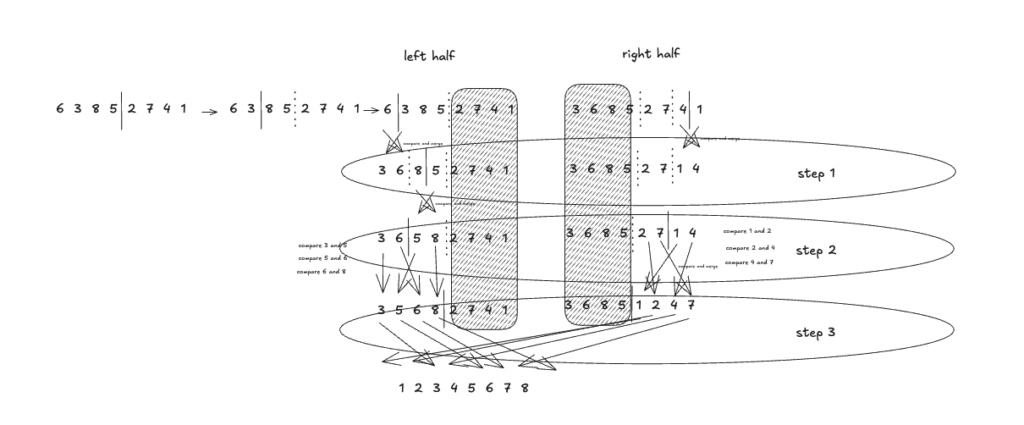
実行時間は、8個の数字では3回のステップがありす。そのステップの中で8回の比較があります。
nに直すと、n * lognとなります。
ビッグO表記ではO(nlogn)となります。
nの2乗の選択ソート、バブルソートと比較するとかなり改善されています。
ビッグΩは最初からソートされていなくても、行うことは全く同じなため、ビッグOと同じく、
Ω(nlogn)です。
トレードオフ
選択ソート、バブルソート、マージソートにおいてはマージソートが最もソートの実行時間が短くできることが期待できます。
ですが、このソート方法はメモリを消費してしまいます。
RAMのメモリの箱からステップとして移動させるときにその分別のメモリスペースを使っているのです。
8までの数字であれば3つのステップがありました。視覚的にわかりやすいように3つのステップを使っていますが、メモリ効率を重視して、3ステップ目は1つ目のステップに値を戻すようにしてあげれば、最大でも2ステップのメモリスペースを確保されていればマージソートを行えます。
つまり、マージソートを行うにはデータ量の2倍のメモリを消費するということです。
マージソートは実行時間とメモリ消費量がトレードオフの関係にあるのです。
トレードオフの関係があるのはマージソートに限りません。
例えば、線形探索とバイナリ検索ではバイナリ検索の方が効率がよいと紹介しました。
ですが、処理の内容はバイナリ検索の方が複雑なため、これを自分で間違いなく実装しようとするとそれなりに時間がかかります。時間をかけて実装するくらいなら簡単だけど実行時間のかかる線形探索を選択してもよいかもしれません。
実行時間と実装時間にトレードオフがあるといえます。
さらに、バイナリ検索をするにはソートされた配列であることが必須でした。
ソートするにしてもそれなりに実行時間がかかることがわかりました。
データ量が少ない場合には、ソートしてからバイナリ検索しなくてもいきなり線形探索をして目的の情報を見つけてもいいかもしれません。
ですが、同様な検索処理をこれから何度も何度も行う場合はその都度線形探索をするよりも、一度ソートをしてしまって、あとはバイナリ検索をした方が効率がいいです。
効率の良さ、消費メモリ、実装の容易性、データ量などさまざまな要因を比較して、目の前の問題を解決するためのもっともバランスのとれた解決策(アルゴリズム)を選択することが重要です。
優れたエンジニアはこのバランス感覚が優れている人であるということがいえるでしょう。


コメント